La physique du monde autour de nous 

Cours de l’Université Inter Ages du Dauphiné

Mercredi 17h à 18h30. Salle B207

Dates : 28 janvier – 4 février – 25 février – 4 mars – 11 mars – 18 mars – 25 mars – 1 avril

 Hôtel de Belmont : 2, square de Belmont – 38000 Grenoble

Des énergies et des mouvements réels dans l’air ou dans l’eau… 
Connaissez-vous la ressemblance entre le vol d’un moustique et d’un Airbus A380 ? La vibration d’une étoile ou d’une goutte d’eau, la puissance d’une chaudière, à quoi sert l’essence dans une voiture ? …et quelle est la durée parfaite pour tremper un biscuit dans le thé ? Pour la méthode, dans un hommage à l’immense physicien Lord Rayleigh (1915), pas de calcul, pas d’équation. Des unités (kg, mètre, seconde, ampère…) et des ordres de grandeur.

Cours 1 du 27 janvier 2026

A – Introduction : Joël Chevrier

  • Joël Chevrier professeur de physique à l’université Grenoble Alpes depuis 1998

ILL/Institut Neel (CNRS-UGA)/ESRF/LIPhy Cambridge/Purdue/Julich(RFA)/Shenzhen/Lisbonne

Physicien expérimentateur : Supraconductivité/Métallurgie/Croissance Cristalline /Surfaces/ Microscopie Champ Proche /Quasicristaux/Casimir/Champ proche thermique/

Aujourd’hui Sensitive Pen 2.0

Innovation pédagogique par le faire – Smartphone = pocketlab

  • Arts et Sciences cf l’autre cours UIAD

Articles Arts&Sciences sur le journal en ligne TheConversation et sur la plateforme du CCSTI de Grenoble Un physicien au musée

B – « La physique du monde autour de nous » comment faire ?

La physique s’occupe de questions universelles: la lumière, l’espace, le temps, la matière, l’énergie, le mouvement, les vibrations… finalement plus ou moins comme tout le monde mais pour la physique, le chemin conduit au quantitatif par l’expérience, la théorie et les unités. Et c’est d’abord par l’expérience.
Comme le disait Richard Feynman : if it disagrees with experiment, it is wrong.
“In general, we look for a new law by the following process: First we guess it; then we compute the consequences of the guess to see what would be implied if this law that we guessed is right; then we compare the result of the computation to nature, with experiment or experience, compare it directly with observation, to see if it works. If it disagrees with experiment, it is wrong. In that simple statement is the key to science. It does not make any difference how beautiful your guess is, it does not make any difference how smart you are, who made the guess, or what his name is — if it disagrees with experiment, it is wrong“

Exemple de la mesure de e/m (J.J. Thomson fin XIX) et de celle de e et m séparées (Millikan début XX)…

Pour travailler ces questions fondamentales, on faite de la mécanique, de l’électromagnétisme, de la thermodynamique, de la physique quantique, de la relativité, de la physique statistique …

Dans ce cours on va se focaliser sur l’analyse dimensionnelle et les unités.

Qu’est qu’on va en faire ?


Des exemples:

  • Sur Terre, l’Everest a une hauteur de 10km environ, 20km pour le mont Olympe sur Mars. Peut on s’en faire une idée avec la physique ?
  • Les oiseaux restent apparemment sans problème sur les lignes à haute tension. Surprenant quand même. Peut on mieux le comprendre par la physique ? (merci Jean Michel Courty)
  • Les tâches d’eau sur les vêtements sont toujours sombres. Quelle bonne raison par la physique ? (merci Julien Bobroff)

Connaissez vous les unités d’un volume, d’une longueur, d’un temps, d’une température, d’une masse, d’un courant électrique, d’une tension électrique, d’une vitesse, d’une accélération, d’une énergie, d’une quantité de chaleur, d’une charge électrique, d’une force, d’une puissance, de h ou h-barre, de kB…

QUIZ : réponse par oui ou non…

QUIZ UIADDownload

Ensuite

temps (seconde)distance parcourue (mètre)
55
1010
1515
2020
2525
3030
3535
4040
4545
5050
5555
6060

Savez vous lire une figure représentant ces données ainsi :

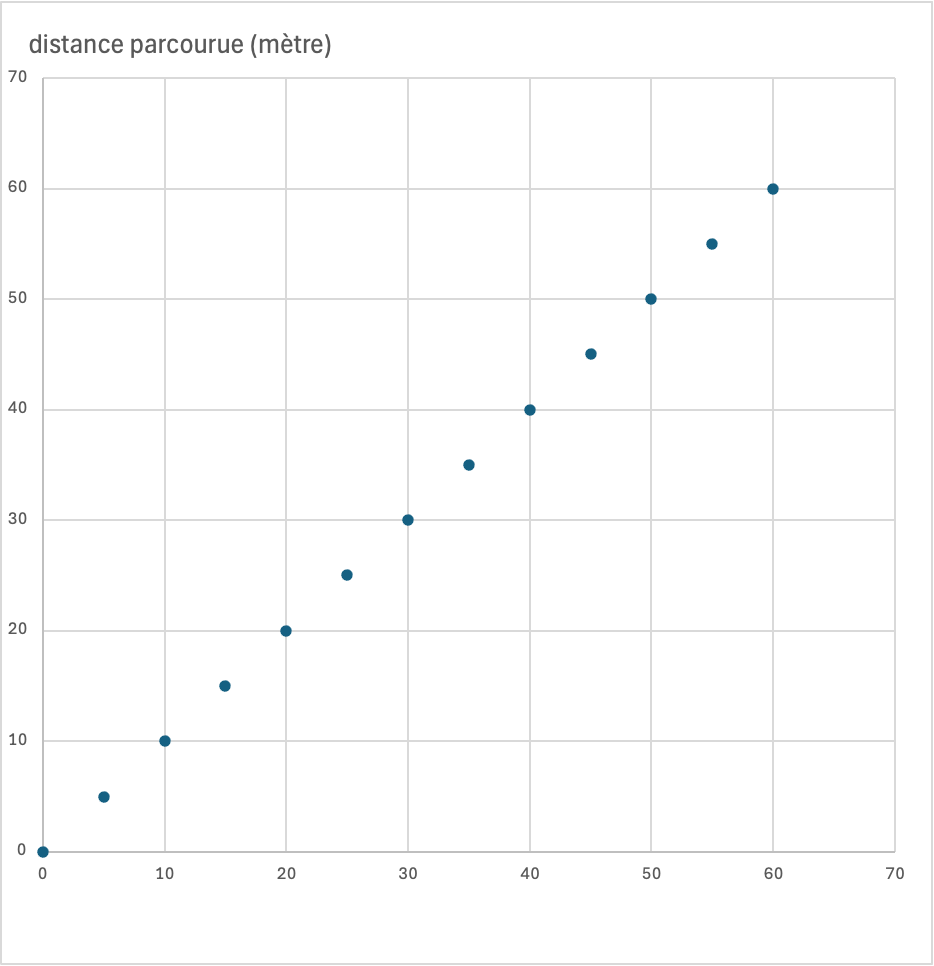
Axe des ordonnées: distance parcourue (mètre) et axe des abscisses: temps (seconde)

Savez vous lire une figure représentant ces données ainsi :

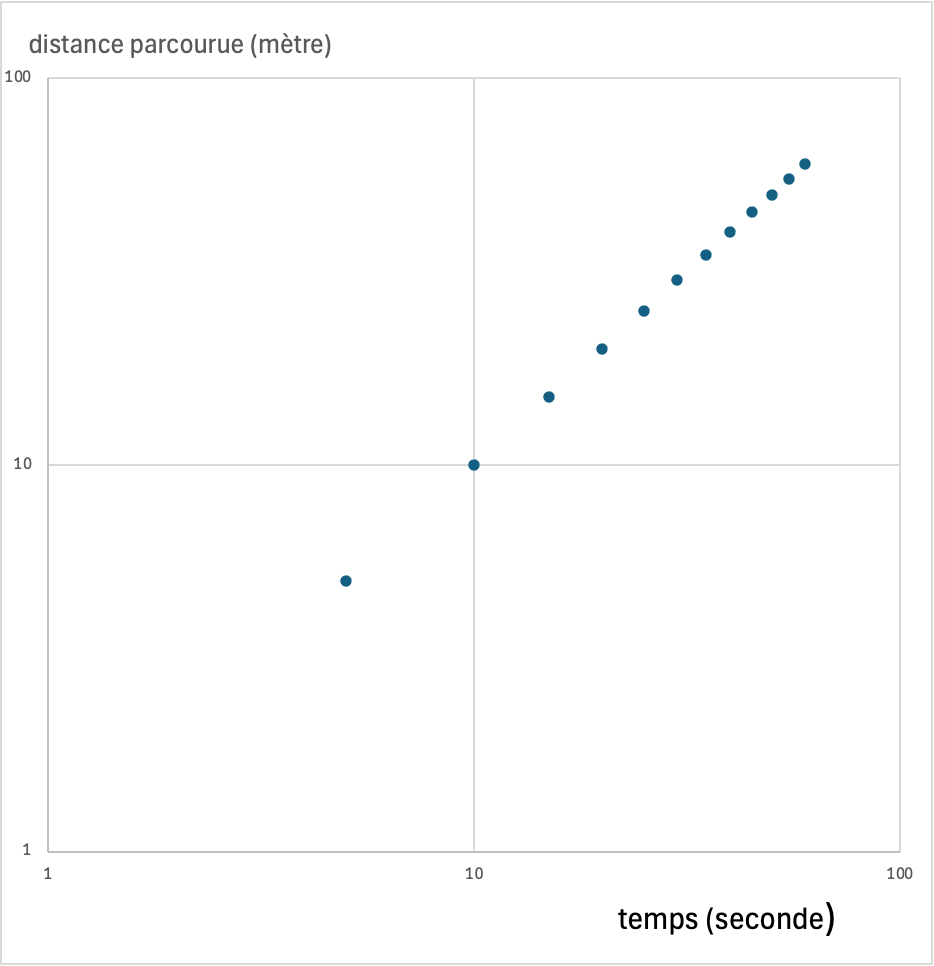
  • La nage des poissons et le vol des oiseaux (d’après Thomas Séon les lois d’échelle Ed.Odile Jacob): nombre de Strouhal (1850-1922) et les hydrauliciens du XIX cf Osborne Reynolds (1842-1912)
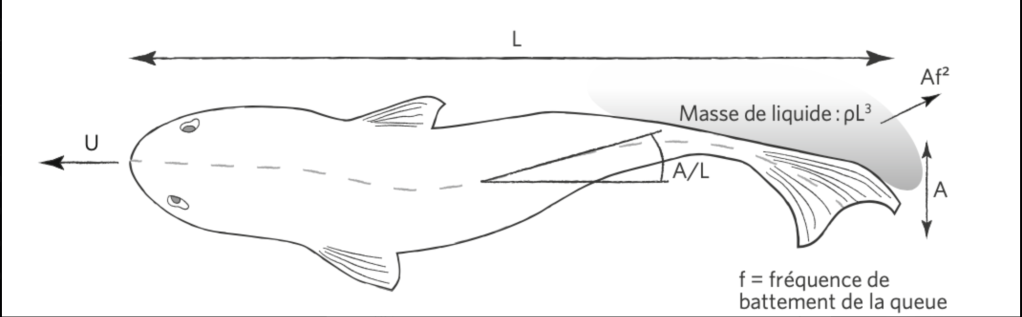
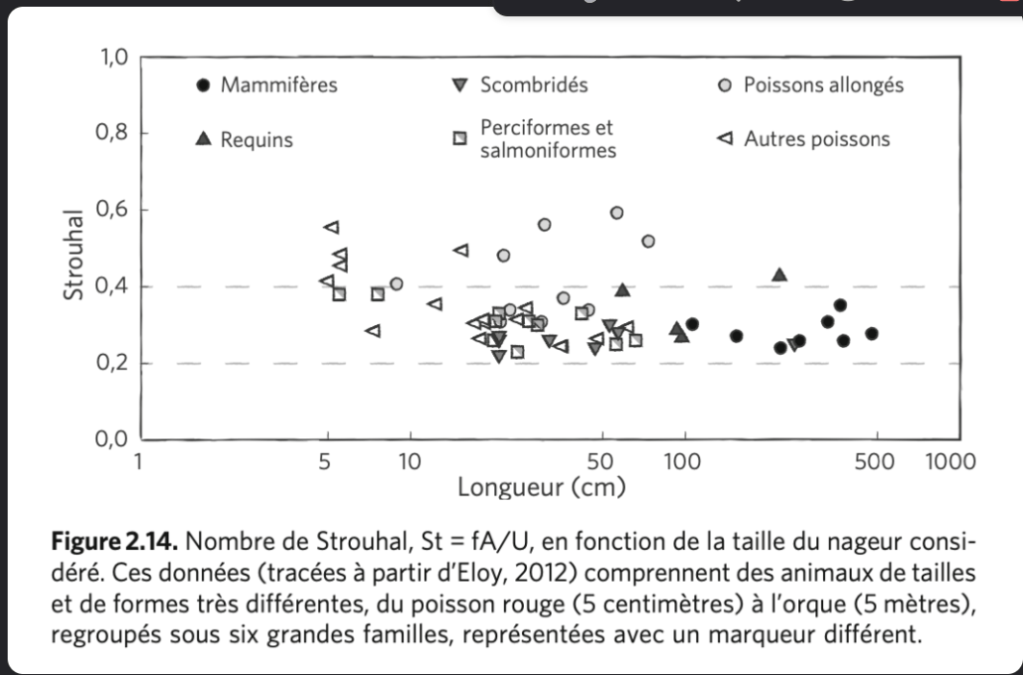
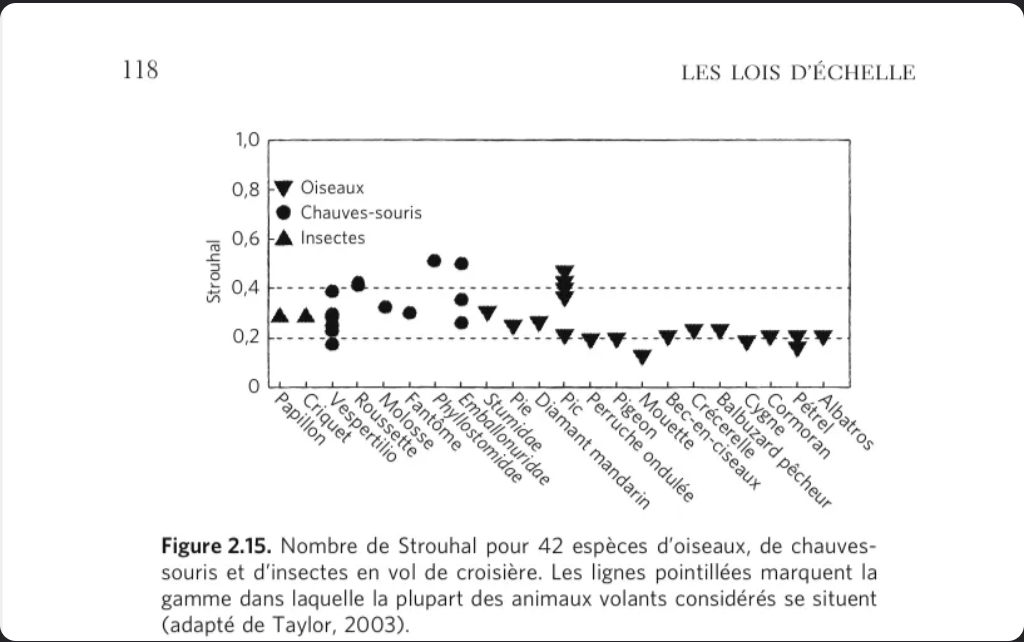
  • Exemples :
  • la vitesse de nage des bactéries
  • nager dans l’eau et courir dans l’air
  • Osborne Reynolds
  • https://www.instagram.com/reel/DOQEIBZDO0W/?igsh=b3JlM3NkNm9uMGpr
  • Le Zeer, le Bojito ou le frigo du désert:
    • l’eau: du liquide à la vapeur et retour
      • faire bouillir de l’eau
      • cuisson à la vapeur
      • évapotranspiration et les rivières volantes (photo Salgado Amazonie)
      • machine à vapeur
      • transpiration
  • La taille des trous dans les gâteaux secs étudiés en les trempant dans le thé
  • La vitesse de l’aviron en fonction du nombre de rameurs : huit rameurs ne vont pas beaucoup plus vite que un seul !
  • La puissance d’une fusée Saturne V au décollage
  • La vibration des étoiles ou des gouttes d’eau
  • L’énergie de la première bombe atomique (cf Geoffroy Taylor)
  • The great flight diagram : quel point commun entre un airbus et un moustique quant au vol ?
  • la taille de l’hydrofoil sous une planche à voile
  • le diamètre d’un éclair
  • la force de la lumière (la pression de radiation)
  • la taille des atomes et la densité de la matière
  • le diamètre des trous noirs
  • la puissance d’un chaudière à la maison
  • la puissance d’une bouilloire
  • La tension de surface de l’eau et la pression dans les bulles (loi de Laplace)
  • L’eau dans le petit monde ou la longueur capillaire ou le mouillage. J. B. S. Haldane (1892‐1964) dans son texte On Being the Right Size (« Une question de taille », 1928) : Un insecte se moque bien de la pesanteur ; il peut tomber sans aucun danger et s’accrocher au plafond sans risque. Il peut se per‐ mettre des systèmes de support extravagants comme les longues pattes de la tipule, mais il est une force qui se révèle aussi redoutable pour l’insecte que la gravité pour les mammifères. C’est la tension superficielle. Un homme sortant du bain entraîne avec lui une couche d’eau de quelques dixièmes de millimètre, qui pèse environ 500 grammes. Une souris sortant de l’eau doit porter l’équivalent de son propre poids. Une mouche, qui doit porter plusieurs fois son poids, se retrouve souvent dans une situation désespérée. Pour un insecte, se désaltérer est aussi risqué que, pour un homme, se pencher au‐dessus d’un précipice pour cueillir un fruit. Si l’insecte est pris par la tension superficielle de l’eau – s’il se mouille –, il a de fortes chances de périr noyé. Quelques insectes, comme le gerris, trouvent le moyen de marcher sur l’eau sans se mouiller, mais la plupart ont développé de longs proboscis (trompes) qui leur permettent d’étancher leur soif à distance.
  • Les physiciens sont paresseux ou la chute dans l’air (avec frottement) par Julien Bobroff
  • D’autres exemples sur le site de Jean Michel Courty Questions de physique
https://www.linkedin.com/posts/julien-bobroff-40449963_voici-une-astuce-diabolique-de-physicien-activity-7335938458282049536-Wo-i?utm_source=share&utm_medium=member_desktop&rcm=ACoAAAXd-0MBVOGMWqyDhyO6beFkv4RbPsWuxfw

pression dans une bulle de savon

_____________________

COURS 2 (4 février 2026) :

Plan:

1- L’eau et les taches sombres pour démarrer
2- les unités de l’accélération et de la force en newton
3- les frottements
– les frottements dans les fluides :
mouvement d’objet, de vivants dans l’air ou dans l’eau
– le frottement solide : frottement de deux surfaces solides

  • Les tâches d’eau sont sombres. Toujours. Pourquoi donc ? Indice optique, réfraction, réflexion totale
    • cf video de Julien !
  • les unités de l’accélération (m.sec-2) et de la force (kg.m.sec-“2)

Vitesse (m.sec-1) en fonction du temps

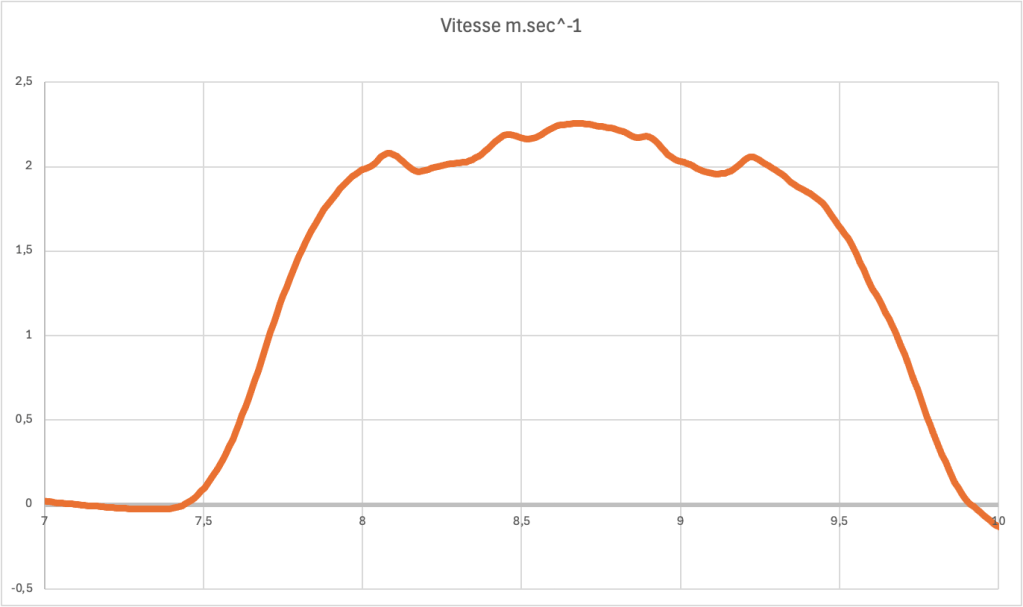
Accélération (m.sec-2) en fonction du temps. L’accélération a est le taux de variation de la vitesse.

Si a=1m.sec-2, la vitesse augmente à chaque seconde de 1m.sec-1=1sec.1m.sec-2

Ci dessous en bleu l’accélération qui correspond à la variation de vitesse présentée dans la courbe ci dessus.

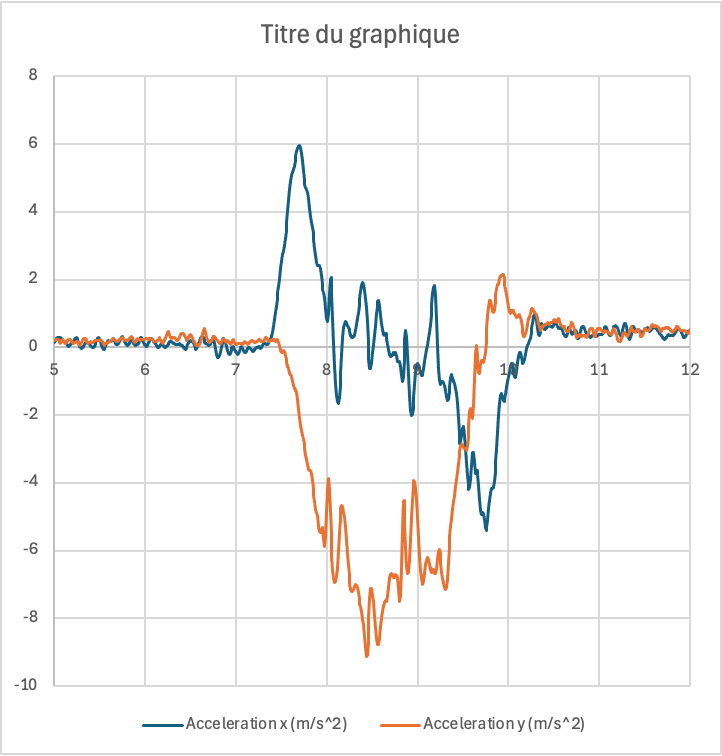
  • les unités de la force (N)
  • Une force F sur un objet de masse m le met en route. L’objet de masse m soumis à cette force F accélère avec une accélération a, sa vitesse V augmente.

Loi de Newton :

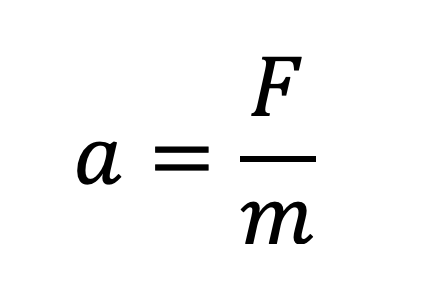
F=a.m, la masse est kg, l’accélération en m.sec-2. Les unités de la force F dans le système international sont kg.m.sec-2. Le newton (N) est donc kg.m.sec-2, quelque soit la nature de la force.

  • le frottement visqueux

Régime de Stokes

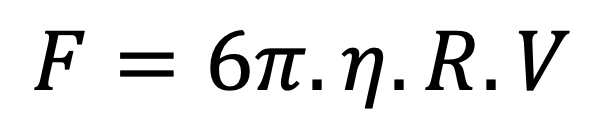
R est le rayon de la sphère en mètre, V est sa vitesse en m.sec-1 et éta la viscosité du fluide en Pa.sec ou N.m-2.sec ou kg.m-1.sec-1

Cette force ne marche pas pour les poissons, les oiseaux, les avions, les voitures, les vélos, les motos, les ballons, les nageurs, les bateaux…
Elle décrit la réalité pour une petite bille d’acier qui tombe dans du glycérine (le TP classique à l’université), la nage des bactéries dans l’eau, les poussières fines dans l’atmosphère… mais pas les bulles de champagne dans l’eau

Pour tout …ou presque…

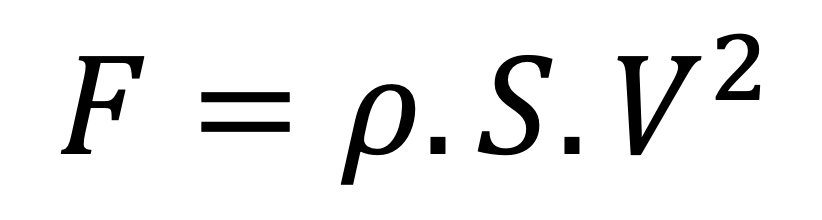
Que l’on complète en (cf Cours de René Moreaux et de Joel Sommeria du LEGI) :

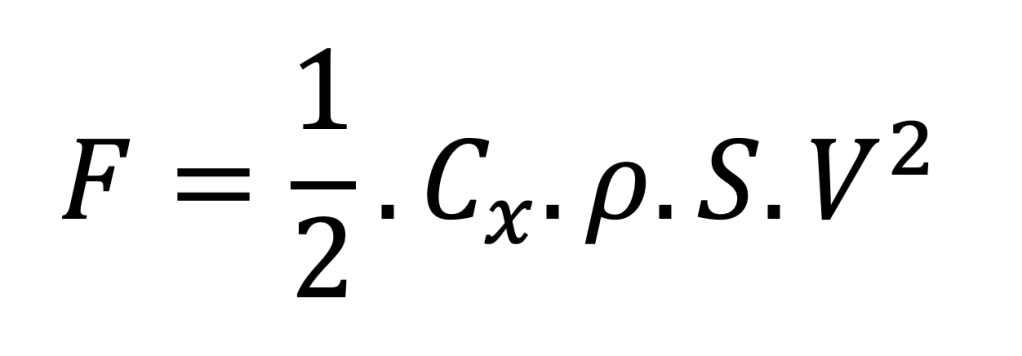
Cx est le coefficient de trainée. L’étude et le contrôle du Cx est une activité qui occupe beaucoup de monde (voiture, avion, bateau, cycliste pro…) cf Balle de golf

  • le frottement (solide) depuis Leonard de Vinci jusqu’à aujourd’hui


Aristote (384-322) – Leonard de Vinci (1452-1519) – Galilée (1564-1642) – Guillaume Amontons (1663-1705)

  • Aristote (très vite, trop vite) : Tout mouvement requiert une cause actuelle et continue. Contrairement à la physique moderne : – il n’existe pas de mouvement par inertie – le repos est l’état naturel par défaut. Un corps ne se meut que tant qu’une cause agit effectivement sur lui.
  • Leonard de Vinci entre Aristote et Galilée
    • LdV1: la force de frottement est proportionnelle à la charge
    • LdV2: la force de frottement est indépendante de l’aire de contact
  • Galilée : principe d’inertie Principe d’inertie (Galilée) : Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme tant qu’aucune force extérieure ne vient modifier cet état. Ou bien: En l’absence de forces (ou lorsque les forces se compensent), un corps conserve une vitesse constante en ligne droite.
  • Toute l’étude du frottement vient ensuite dans une physique « galiléenne ». Au lycée ou en licence, une phrase magique est : « pour étudier ce mouvement, on négligera les frottements… »
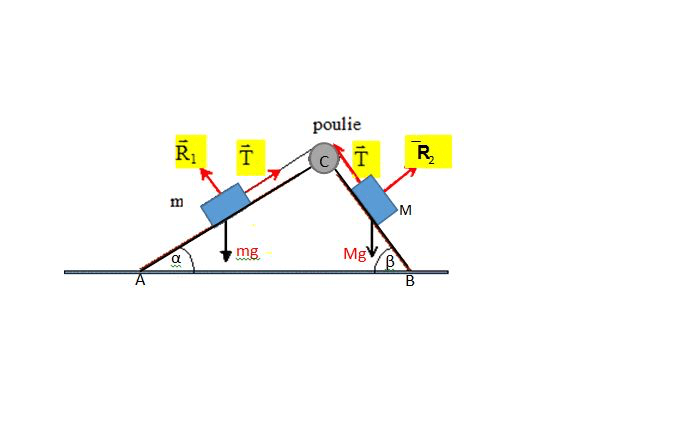
  • Les propriétés élémentaires du frottement de glissement (solide contre solide) ont été (re)découvertes expérimentalement entre le XVe et le XVIIIe siècle et ont été formulées sous la forme de trois lois empiriques :

Première loi d’Amontons : La force de frottement est directement proportionnelle à la charge appliquée.

Deuxième loi d’Amontons : La force de frottement est indépendante de l’aire apparente de contact.

Loi de Coulomb du frottement : Le frottement cinétique est indépendant de la vitesse de glissement.

Ensuite Bowden et Tabor à Cambridge (1930-1950)

  • Le contact réel entre deux surfaces est très inférieur au contact apparent.
  • Les surfaces sont rugueuses à toutes les échelles.
  • Le contact se fait via des micro-jonctions plastiques.

Alors on cherche :

  1. à faire frotter des surfaces atomiquement plates comme deux surfaces de mica fraichement clivé
  2. à construire un contact ponctuel entre une pointe et une surface
  3. à étudier le comportement avec les surfaces telles quelles !

Les 3 ont été mis en oeuvre et le sont encore aujourd’hui.

Solution 1 à la suite de Bowden et Tabor à Cambridge : D. Tabor, R.H.S. Winterton, J.N. Israelachvili ont construit le surface force apparatus

Solution 2: à la suite du prix Nobel 1986, le microscope à force atomique 

Solution 3: on fait frotter un patin sur une surface encore et toujours…

Le stick-slip motion :

https://cahier-de-prepa.fr/mp2i-fauriel/download?id=3445

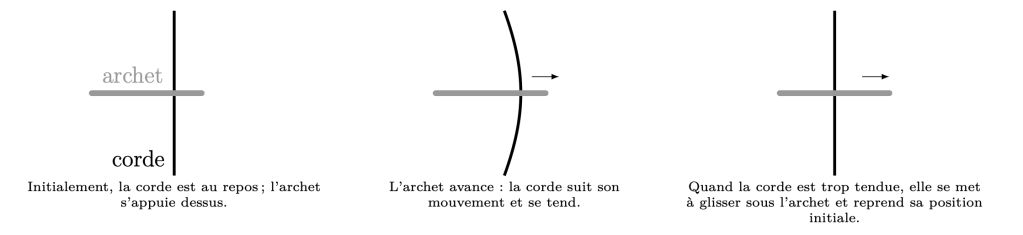
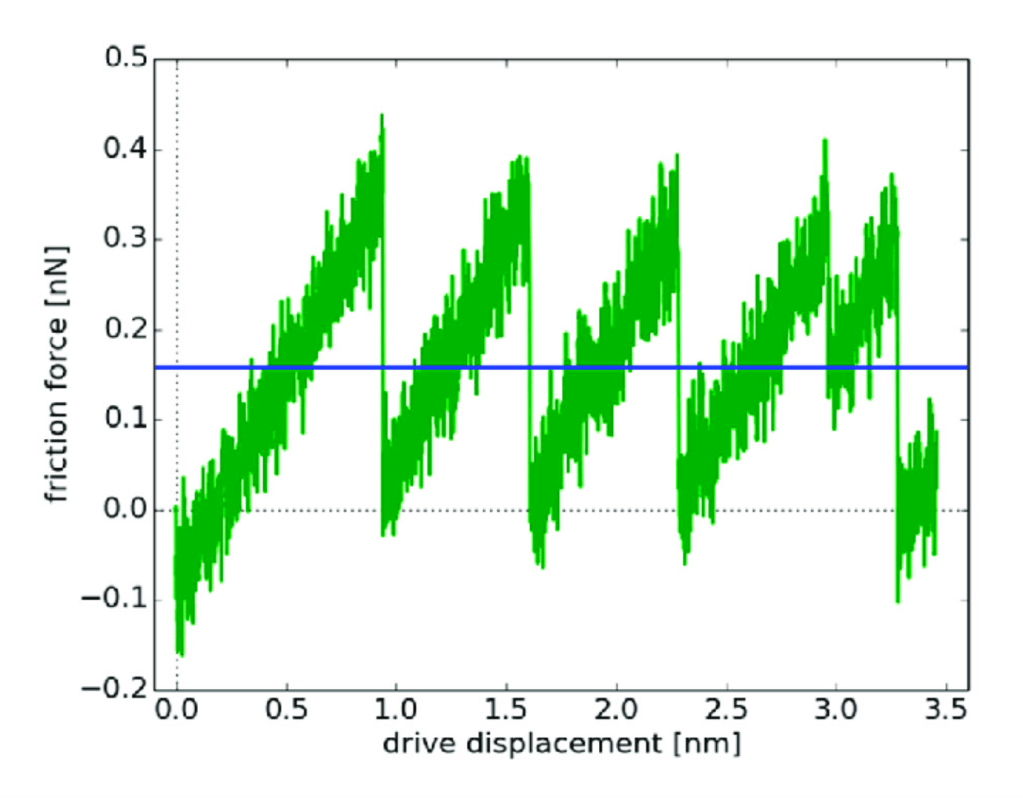
La mécanique classique et le frottement

  • Les équations de Newton sont réversibles dans le temps.
  • Le frottement introduit une dissipation irréversible.

Conclusion:

Léonard : découverte empirique sans théorie,

Amontons–Coulomb : formalisation phénoménologique,

XIXᵉ siècle : dissipation, irréversibilité…

XXᵉ siècle : microphysique du contact

Aujourd’hui : L’étude du frottement solide, la tribologie, est un champ de recherche interdisciplinaire : physique, mécanique, chimie, science des matériaux, géologie… avec des phénomènes non linéaires, dissipatifs, hors équilibre, multi-échelles (rugosité, multi-contacts…).